The QRcode

This code is part of the family of 2-dimensional codes, it can encode up to 7089 characters on a very small surface. The encoding is done in two steps : first the datas are converted into a bit stream cut into codewords. (High level encoding) then these are converted into small black and white squares. In addition, an error correction system makes it possible to reconstruct badly printed, erased, fuzzy or torn off datas. In the remainder of this presentation, the term "codeword" will be abbreviated to CW and Reed-Solomon code in RS. There are also micro QR codes not studied here.

The general structure.

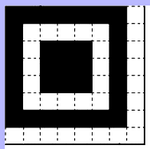
The symbol is a square array consisting of rows and columns (Numbered from 0). Each cell is a small black or white square called module. The symbol has 3 finder patterns at the top and bottom left corners making it well recognizable. The dimension of the symbol is called the version, there are 40 with 21 to 177 modules (In steps of 4 modules). The correction level (Among 4) is denoted L, M, Q or H
Colors can be switched : white on black ; the symbol can also be mirrored.
Extended Channel Interpretation (ECI) provides a mode for specifying a particular interpretation of byte values or for identifying a particular code page.
By default the ECI code is 000003 which designates the Latin alphabet ISO 8859-1.
If necessary, a mechanism allows more data to be spread over several symbols. (Up to 16)
The error correction mechanism is based on Reed-Solomon codes.
The symbol has a number of function modules :
- The 3 finder patterns of 8 x 8 modules
- Alignment patterns of 5 x 5 modules (Position : see table)
- 2 timing patterns : band alternating white and black module, in horizontal line 6 and in vertical column 6
- Format and version information zones contiguous to the finder patterns
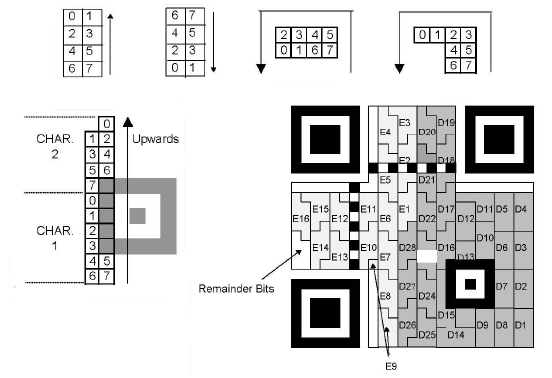
The function modules (patterns, synchro, info, ...) being placed, the data are placed starting from the bottom right corner going from right to left, first by going up and down and bypassing all the modules of function.
A white margin of 4 modules must frame the code.

Low level encoding.

There are 40 versions (Sizes) of symbol. A set of parameters is attached to each version :

The version number.
The first spacing of the alignment patterns
The second spacing of alignment patterns
The number of bits for the 4 size indicators in numeric, alphanumeric, byte, and Kanji mode (See High Level Encoding)
For each of the 4 levels of error correction (See High Level Encoding)
- The number of blocks in which to distribute the data
- The number of RS per block

From these parameters we can calculate other values, this is done using a spreadsheet :

We will find the calculation of the size of the symbol, the number and location of alignment patterns, the areas occupied by the various elements, etc ...
To build a QRcode you need :

Place the 3 finder patterns at the top and bottom left corners.
The markers have a size of 8 x 8, counting a margin of 1 module on the 2 internal sides ; see below the upper left corner :

Draw timing lines on line and column 6
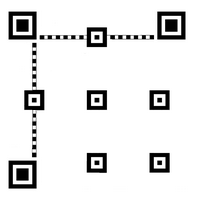
Place the alignment patterns. These have a size of 5 X 5.
Their center is placed at the intersection of a grid whose line numbers are identical to the column numbers, we will call these numbers L / C thereafter.
The first L / C is always 6. The 3 marks that collide with the corner marks are removed.
For example in the drawing below we have 3 L / C, the number of patterns is (3 x 3) -3 = 6. With 4 L / C we would have (4 x 4) - 3 = 13 marks.
There are 2 spacing columns in the spreadsheet to use as follows :
- 2nd L / C = 6 (which is the 1st L / C) + spacing 1
- 3rd L / C (and following) = L / C previous + spacing 2

Reserve locations for format information.
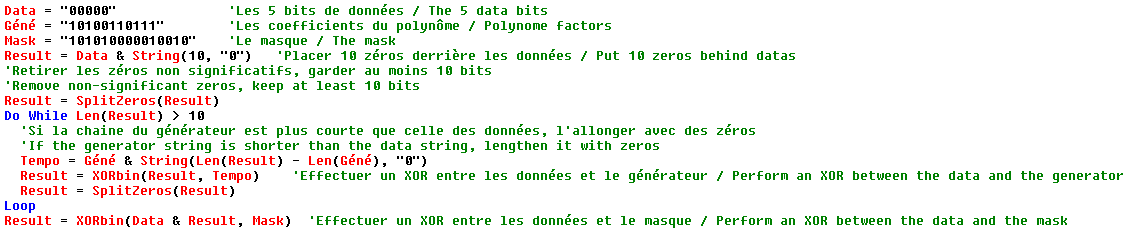
The format information is a sequence of 15 bits: 5 data and 10 BCH type error correction codes.
The 5 data bits are :
   2 bits indicating the correction level of the code : L (01), M (00), Q (11) or H (10)
   3 bits indicating the mask pattern used (see below for masking)
The 10 correction bits are calculated as follows :
   The 5 data bits are the coefficients of a polynomial of order 14; example 01001 gives X¹³ + X¹⁰
   We divide this polynomial by X¹⁰ + X⁸ + X⁵ + X⁴ + X² + X + 1 (The coefficients of this polynomial are : 10100110111)
   The coefficients of the remainder of the division are the 10 correction bits to be added to the 5 data bits.
Finally we apply the mask 101010000010010 by doing a XOR with the 15 bits obtained previously.

Format information is placed in 2 places with a total of 31 modules (1 of which is always black)

The algorithm for creating the format string in Basic :
For version 7 and above, you must add version information.
The version information is a 18-bit sequence : 6 data bits and 12 Golay error correction codes.
The 6 data bits represent the version number.
The 12 correction bits are calculated as follows :
   The 6 data bits are the coefficients of a polynomial of order 17 ; example for version 9 : 001001 gives X¹⁵ + X¹²
   We divide this polynomial by X¹² + X¹¹ + X¹⁰ + X⁹ + X⁸ + X⁵ + X² + 1
   The coefficients of the remainder of the division are the 12 correction bits to be added to the 6 data bits.

The version information is placed in 2 places occupying a total of 36 modules

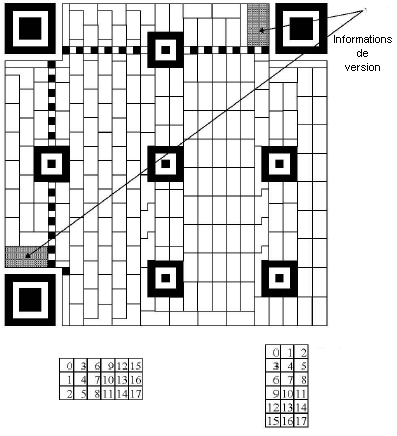
The algorithm for creating the version string in Basic :
Now let's go to the placement of the data and correction modules, we start in the lower right corner and up on 2 columns of modules. The bits of each CW are placed starting from the last one. The bits are placed first in the right column and then in the left column and the function modules are bypassed. Arrived at the top we go down on the 2 adjacent columns on the left always in right-left order.
In order to obtain a bar code as balanced as possible it is now necessary to apply a mask to the area of the data. Masking consists of applying a XOR operation between the data of each module and the corresponding module of the mask.
There are 8 different masks and we will have to find the one that gives the most balanced result :
- White report on black close to 1
- If possible, no further 1011101
- As few "big" blocks as possible.
The number of the selected mask will be indicated in the format information. In the following table are the 8 types of mask with the function to define the pattern of the mask. Any module for which the condition is true will be black. In the condition formula i and j are respectively the line and column number of the module. i = j = 0 corresponds to the upper left corner.

Mask number	Condition
000	(i + j) MOD 2 = 0
001	i MOD 2 = 0
010	j MOD 3 = 0
011	(i + j) MOD 3 = 0
100	((i DIV 2) + (j DIV 3)) MOD 2 = 0
101	(i j) MOD 2 + (i j) MOD 3 = 0
110	((i j) MOD 2 + (i j) MOD 3) MOD 2 = 0
111	((i + j) MOD 2 + (i j) MOD 3) MOD 2 = 0

High level encoding.

We will use the following operators : + -> addition, x -> multiplication, \ -> integer division, MOD -> rest of the whole division
There are 4 encoding modes (Compression) that can be mixed :

Compression mode	Data to be encoded	Compression rate	Mode indicator
Numeric	ASCII digits	3 digits in 10 bits	0001
Alphanumeric	Digits + capital letters + 9 symbols	2 characters in 11 bits	0010
Byte	Byte	1 byte in 8 bits	0100
Kanji	Asian characters	/	1000

There are other indicators not studied here: 0111 = ECI, 0011 = Multi codes, 0101 and 1001 = FNC1
0000 indicate the end of datas.

Each segment begins with a 4-bit mode indicator followed by the number of characters encoded on a variable bit number (see table), followed by the data.

The segments of each mode are then concatenated followed by a terminator composed of 4 zeros which is the end of data indicator.
The terminator can be abbreviated if it allows the complete filling of the data area of the symbol.
This stream is then cut into 8-bit CW. If necessary, the last CW is adjusted to 8 bits by adding bits 0. If the number of CWs does not completely fill the symbol add 11101100 then 00010001 and start again (236 and 17 in decimal)
The CWs are then divided into a number of blocks (see table) The size of the blocks can vary by one unit; for example 46 CWs divided into 4 blocks will give 2 blocks of 11 and 2 blocks of 12. In this case, we will place the smaller blocks first.
For each block the Reed Solomon codes are calculated.

Finally we will interleave the data then the RS codes as follows :
n is the number of blocks, m the number of CWs in each block and z the number of RS codes per block
data 1 of block 1 - data 1 of block 2 - ... - data 1 of block n
data 2 of block 1 - data 2 of block 2 - ... - data 2 of block n
...
data m of block 1 - data m of block 2 - ... - data m of block n
then :
RS 1 of block 1 - RS 1 of block 2 - ... - RS 1 of block n
RS 2 of block 1 - RS 2 of block 2 - ... - RS 2 of block n
...
RS z of block 1 - RS m of block 2 - ... - RS z of block n

The numeric mode.
In this mode the datas are divided into groups of 3 digits which are compressed in 10 bits.
If only 2 digits remain, we convert them to 7 bits and if only one digit remains, we convert it to 4 bits. The segment will therefore include : the mode indicator 0001, the character counter (Length to be taken in the table) and the data.

Exemple :
Chain : 34567
First group : 345 ie 0101011001
2nd group : 67 ie 1000011
Number of characters : 5
If version code 3 for example, length on 9 bits, ie: 000000101
Segment : 0001 000000101 0101011001 1000011

Alphanumeric mode.
In this mode we can only encode 45 characters numbered 0 to 44 according to the following table :

Value	Character	Value	Character	Value	Character	Value	Character
0	0	13	D	26	Q	39	*
1	1	14	E	27	R	40	+
2	2	15	F	28	S	41	-
3	3	16	G	29	T	42	.
4	4	17	H	30	U	43	/
5	5	18	I	31	V	44	:
6	6	19	J	32	W
7	7	20	K	33	X
8	8	21	L	34	Y
9	9	22	M	35	Z
10	A	23	N	36	(Espace)
11	B	24	O	37	$
12	C	25	P	38	%

The characters are taken in pairs and encoded on 11 bits. The code of the first character is multiplied by 45, then the code of the 2nd character is added and the sum is converted into 11-bit binary.
If a single character remains, its code is converted to a 6-bit binary.

Exemple :
Chain : ZEBU : 35 14 11 30
First group : 35 x 45 + 14 = 1589 ie 11000110101
2nd group : 11 x 45 + 30 = 525 ie 01000001101
Number of characters : 4
If version code 3 for example, length on 10 bits, ie: 0000000100
Segment : 0010 0000000100 11000110101 01000001101

Byte mode.
This mode can encode any byte.
These are simply converted to binary.
Kanji mode.
This mode is not studied here.

Detection and correction of errors.

The system of correction is based on the codes of " Reed Solomon " which make the joy of the mathematicians and the terror of the others ...
The number of correction CWs depends on the version of the code and the level of correction chosen, it is given for each block of data. (See table)
The Reed Solomon codes use a polynomial in which the power of x is the number of error correction CWs used. For example, for a code version 1 with correction level L we use an equation to obtain 7 RS like this : x⁷ + ax⁶ + bx⁵ + cx⁴ + dx³ + ex² + fx + g The numbers a, b, c, d, e, f and g are the coefficients of the polynomial equation.

For information the equation is : x⁸ + x⁴ + x³ + x² + 1 and the Galois body is modulo 285.
There are 36 Reed Solomon code block sizes (see table) including micro-codes. The coefficients of these 36 polynomial equations have been precalculated. You can see the coefficient file. We can also calculate them. But first a small explanation on the operations in a Galois body.

Arithmetic operations in a Galois body of characteristic 2.

The sum and the difference are the same function : the exclusive OR function.
A + B = A - B = A Xor B
The multiplication is more complicated ; first we need to create 2 tables containing the Logs and Antilogs of the body according to its "modulo" (Here 285) :

Now we can calculate Mult(a, b) = Alog((Log(a) + Log(b)) Mod 255)

Here is now in Basic the algorithm to calculate the factors :

And now, still in Basic, the algorithm for calculating correction CWs.

Find all the RS code calculations of the different 2D barcodes in Visual Basic 6.
It is a ZIP file without installation :

Those who have read and understood the codes of Reed Solomon will find themselves there ; for the few ignorant who have not understood everything (like me!) It will be enough to apply the "recipe" by using the codes obtained in the reverse order (last to first).

The creation of barcodes.

Now that we know how to create a barcode pattern, we still have to draw it on the screen and print it on paper. Two approaches are possible :

The graphic method where each bar is "drawn" like a solid rectangle. This method makes it possible to calculate the width of each bar to the nearest pixel and to work on multiples of the width of a pixel of the used device. This gives good accuracy especially if the device has a low density as is the case of screens and inkjet printers. This method require special programming routines and does not allow to make bar codes with a current software.
The special font in which each character is replaced by a bar code. This method allow the use of any software like a text processing or a spreadsheet. (For example LibreOffice, the free clone of MSoffice !) The scale settings according to the selected size can bring small misshaping of the bar drawing. With a laser printer there's no probs.

It seems there is no free font for QRcode on the net. The font used for Datamatrix codes may be perfectly suitable. It consists of 16 combinations assigned to the first 16 capital letters.
If we give a value to each point of this 2 X 2 matrix like this :

1	2
4	8

The ASCII value of the character associated with a given matrix is the sum of the values of each point + 65 (65 = A = no point!)

The font " datamatrix.ttf " (Suitable for QRcodes)

This font contains the 16 characters A (ASCII: 65) to P (ASCII: 80)

Copy this file
in the directory of
fonts, most often :
C:\WINDOWS\FONTS

Encoding a QRcode

The program will have to take place in several stages :

Compacting the data in the CWs using the different modes and trying to optimize, and if necessary adding the stuffing.
Determination of the version (Size) of the code.
Placement of all function modules (Except for format information).
Cut into blocks if necessary then calculate correction CWs according to the version and the level of correction chosen.
Placement of CWs in the matrix.
Application of the different masks and choice of it after evaluation of the results.
Calculation and placement of format information.
Transform each pair of lines into a string of characters. The length of the string is: number of modules / 2. The number of line (or column) being odd, we add to the right and bottom a line of white modules.

Because of the interaction between the different modes of compression it is difficult to make a 100% optimization. However, the standard gives in Appendix J a method of optimization ...
The evaluation of the results of the different masks will be done "by eye" and by testing the codes obtained.

A little program to test all that.

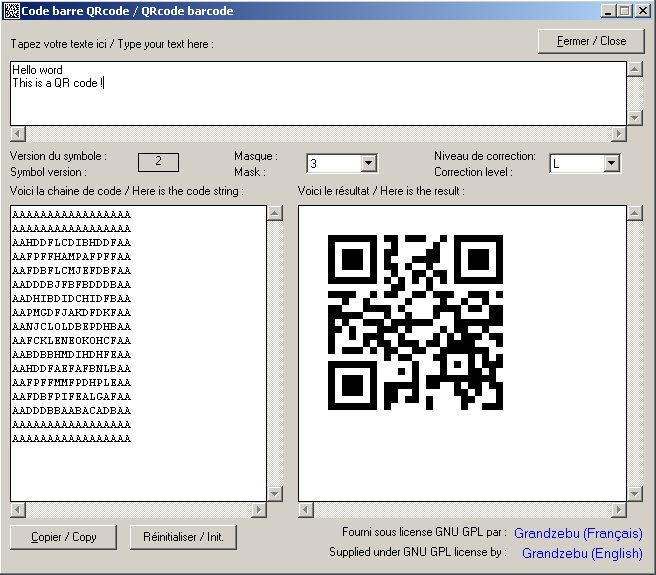
WORK IN PROGRESS

The function QRcode$ is about 900 lines, so I do not reproduce it here, just get it in the file "form1.frm" which is with the program above ; with the self-installation program the file "form1.frm" is located in the program directory, subdirectory "sources". The function is called as follows :
resultat$ = QRcode$(Chaine$, Level%, Mask%, Version%, CodeErr%) with Chaine$ which must contain the string to encode, Level% for the correction level, Mask% for the mask to use. On return Version% will give the code version (size) used and CodeErr% a possible error number. These last two parameters are optional and are passed by references.
Values of CodeErr% at the return of the function : 1: Chaine$ is empty 2: Chaine$ contains too much data.
You just have to display or print the result string with the Datamatrix font for example in a word processor. Word users will even be able to integrate the QRcode$ function into a macro to automate the process. To achieve all the treatments in a single function, I had to use "Gosub" instead of functions with parameters ; I can already hear the programming esthetes screaming sacrilegious !

Do you like this page ?

Is it useful to you ?

Index des mots-clés

The QR Code